📌 Perceptron란?
퍼셉트론(Perceptron)은 생물학적 뉴런을 수학적으로 모델링한 인공 뉴런 모델로, 여러 입력 신호를 받아 각 입력에 대한 가중치(Weight)를 곱한 후, 이들의 가중합(Weighted Sum)을 계산하고, 활성화 함수(Activation Function)를 통해 최종 출력을 결정하는 구조이다.
🔧 구조 (Perceptron Structure)
입력(x) → 가중치(w) → 가중합(∑) → 활성화 함수(f) → 출력(y)
- 입력 (Input): AND, OR 등 논리 연산을 위한 입력 신호.
- 가중치 (Weight): 입력 신호의 중요도를 결정하며, 학습을 통해 조정됨.
- 가중합 (Weighted Sum): 각 입력과 그에 대응하는 가중치의 곱을 모두 더한 값.
- 활성화 함수 (Activation Function): 가중합이 임계값을 넘으면 1, 넘지 못하면 0을 출력하는 함수. 대표적으로 단위 계단 함수 사용.
- 출력 (Output): 최종 결과값 (보통 0 또는 1의 이진 출력).
🎯 요약
- 퍼셉트론은 이진 분류 문제를 해결할 수 있는 가장 기본적인 신경망 구조이다.
- 학습을 통해 입력 신호의 중요도를 나타내는 가중치가 조정된다.
- 단층 퍼셉트론은 선형 분리 가능한 문제만 해결할 수 있다.
👨💻 실습
💡 Code : AND & OR & NAND & XOR Gate Perceptron
# AND & OR & NAND & XOR Gate Perceptron
import numpy as np
import matplotlib.pyplot as plt
class Perceptron:
def __init__(self, input_size, lr=0.1, epochs=10):
self.weights = np.zeros(input_size)
self.bias = 0
self.lr = lr
self.epochs = epochs
self.errors = []
def activation(self, x):
return np.where(x > 0, 1, 0)
def predict(self, x):
linear_output = np.dot(x, self.weights) + self.bias
return self.activation(linear_output)
def train(self, X, y):
for epoch in range(self.epochs):
total_error = 0
for xi, target in zip(X, y):
prediction = self.predict(xi)
update = self.lr * (target - prediction)
self.weights += update * xi
self.bias += update
total_error += int(update != 0.0)
self.errors.append(total_error)
print(f"Epoch {epoch+1}/{self.epochs}, Errors: {total_error}")
# AND 게이트 데이터 및 학습
X_and = np.array([[0,0],[0,1],[1,0],[1,1]])
y_and = np.array([0,0,0,1])
print(" AND Gate Training")
ppn_and = Perceptron(input_size=2)
ppn_and.train(X_and, y_and)
print("\n AND Gate Test:")
for x in X_and:
print(f"Input: {x}, Predicted Output: {ppn_and.predict(x)}")
# OR 게이트 데이터 및 학습
X_or = np.array([[0,0],[0,1],[1,0],[1,1]])
y_or = np.array([0,1,1,1])
print("\n OR Gate Training")
ppn_or = Perceptron(input_size=2)
ppn_or.train(X_or, y_or)
print("\n OR Gate Test:")
for x in X_or:
print(f"Input: {x}, Predicted Output: {ppn_or.predict(x)}")
# NAND 게이트 데이터 및 학습
X_nand = np.array([[0,0],[0,1],[1,0],[1,1]])
y_nand = np.array([1,1,1,0]) # AND와 반대
print("\n NAND Gate Training")
ppn_nand = Perceptron(input_size=2)
ppn_nand.train(X_nand, y_nand)
print("\n NAND Gate Test:")
for x in X_nand:
print(f"Input: {x}, Predicted Output: {ppn_nand.predict(x)}")
# XOR 게이트 데이터 및 학습
X_xor = np.array([[0,0],[0,1],[1,0],[1,1]])
y_xor = np.array([0,1,1,0]) # 선형 분리 불가능
print("\n XOR Gate Training")
ppn_xor = Perceptron(input_size=2)
ppn_xor.train(X_xor, y_xor)
print("\n XOR Gate Test:")
for x in X_xor:
print(f"Input: {x}, Predicted Output: {ppn_xor.predict(x)}")
✅ Result : AND & OR & NAND & XOR Gate Perceptron
AND Gate Training
Epoch 1/10, Errors: 1
Epoch 2/10, Errors: 3
Epoch 3/10, Errors: 3
Epoch 4/10, Errors: 2
Epoch 5/10, Errors: 1
Epoch 6/10, Errors: 0
Epoch 7/10, Errors: 0
Epoch 8/10, Errors: 0
Epoch 9/10, Errors: 0
Epoch 10/10, Errors: 0
AND Gate Test:
Input: [0 0], Predicted Output: 0
Input: [0 1], Predicted Output: 0
Input: [1 0], Predicted Output: 0
Input: [1 1], Predicted Output: 1
OR Gate Training
Epoch 1/10, Errors: 1
Epoch 2/10, Errors: 2
Epoch 3/10, Errors: 1
Epoch 4/10, Errors: 0
Epoch 5/10, Errors: 0
Epoch 6/10, Errors: 0
Epoch 7/10, Errors: 0
Epoch 8/10, Errors: 0
Epoch 9/10, Errors: 0
Epoch 10/10, Errors: 0
OR Gate Test:
Input: [0 0], Predicted Output: 0
Input: [0 1], Predicted Output: 1
Input: [1 0], Predicted Output: 1
Input: [1 1], Predicted Output: 1
NAND Gate Training
Epoch 1/10, Errors: 2
Epoch 2/10, Errors: 3
Epoch 3/10, Errors: 3
Epoch 4/10, Errors: 0
Epoch 5/10, Errors: 0
Epoch 6/10, Errors: 0
Epoch 7/10, Errors: 0
Epoch 8/10, Errors: 0
Epoch 9/10, Errors: 0
Epoch 10/10, Errors: 0
NAND Gate Test:
Input: [0 0], Predicted Output: 1
Input: [0 1], Predicted Output: 1
Input: [1 0], Predicted Output: 1
Input: [1 1], Predicted Output: 0
XOR Gate Training
Epoch 1/10, Errors: 2
Epoch 2/10, Errors: 3
Epoch 3/10, Errors: 4
Epoch 4/10, Errors: 4
Epoch 5/10, Errors: 4
Epoch 6/10, Errors: 4
Epoch 7/10, Errors: 4
Epoch 8/10, Errors: 4
Epoch 9/10, Errors: 4
Epoch 10/10, Errors: 4
XOR Gate Test:
Input: [0 0], Predicted Output: 1
Input: [0 1], Predicted Output: 1
Input: [1 0], Predicted Output: 0
Input: [1 1], Predicted Output: 0
💡 Code : 경계 결정 시각화 함수 (AND, OR, NAND, XOR)
# 경계 결정 시각화 함수 (AND, OR, NAND, XOR)
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import numpy as np
def plot_decision_boundary(X, y, model, title='Perceptron Decision Boundary'):
cmap_light = ListedColormap(['#FFDDDD', '#DDDDFF']) # 배경 색상
cmap_bold = ListedColormap(['#FF0000', '#0000FF']) # 점 색상
h = .02 # mesh grid 간격
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(figsize=(6, 5))
plt.contourf(xx, yy, Z, cmap=cmap_light)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold,
edgecolor='k', s=100, marker='o')
plt.xlabel('Input 1')
plt.ylabel('Input 2')
plt.title(title)
plt.grid(True)
plt.show()
# AND 게이트 결정 경계 시각화
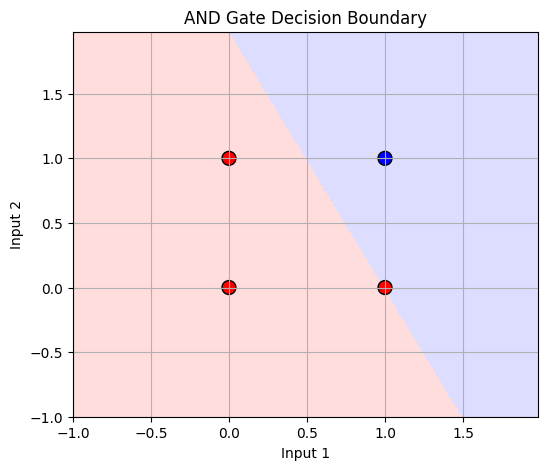
plot_decision_boundary(X_and, y_and, ppn_and, title='AND Gate Decision Boundary')
# OR 게이트 결정 경계 시각화
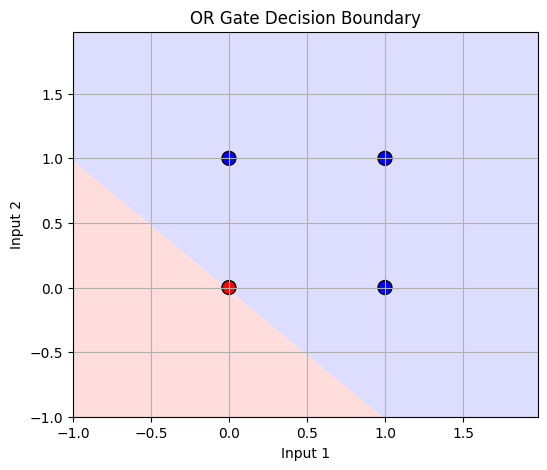
plot_decision_boundary(X_or, y_or, ppn_or, title='OR Gate Decision Boundary')
# NAND 게이트 결정 경계 시각화
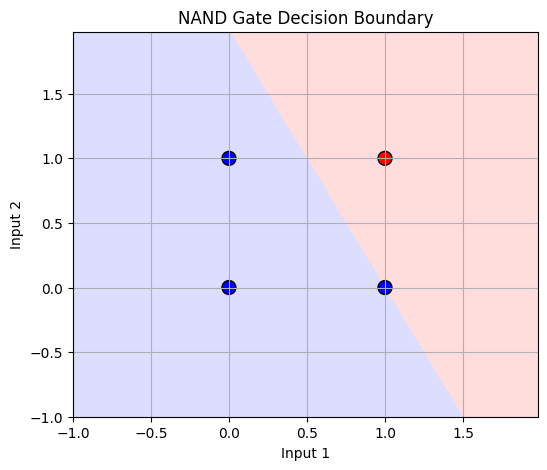
plot_decision_boundary(X_nand, y_nand, ppn_nand, title='NAND Gate Decision Boundary')
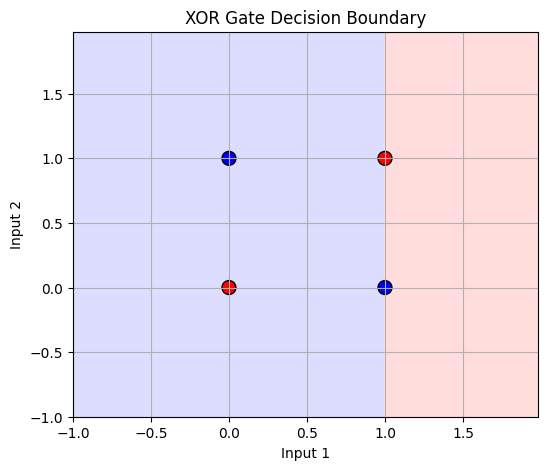
# XOR 게이트 결정 경계 시각화
plot_decision_boundary(X_xor, y_xor, ppn_xor, title='XOR Gate Decision Boundary')
✅ Result : 경계 결정 시각화 함수 (AND, OR, NAND, XOR)
💡 Code : # 오류 시각화 (AND, OR, NAND, XOR)
# 오류 시각화 (AND, OR, NAND, XOR)
plt.figure(figsize=(8, 5))
plt.plot(range(1, len(ppn_and.errors) + 1), ppn_and.errors, marker='o', label='AND Gate')
plt.plot(range(1, len(ppn_or.errors) + 1), ppn_or.errors, marker='s', label='OR Gate')
plt.plot(range(1, len(ppn_nand.errors) + 1), ppn_nand.errors, marker='^', label='NAND Gate')
plt.plot(range(1, len(ppn_xor.errors) + 1), ppn_xor.errors, marker='x', label='XOR Gate')
plt.xlabel('Epochs')
plt.ylabel('Number of Errors')
plt.title('Perceptron Learning Error Over Epochs')
plt.legend()
plt.grid(True)
plt.show()
✅ Result : 오류 시각화 (AND, OR, NAND, XOR)
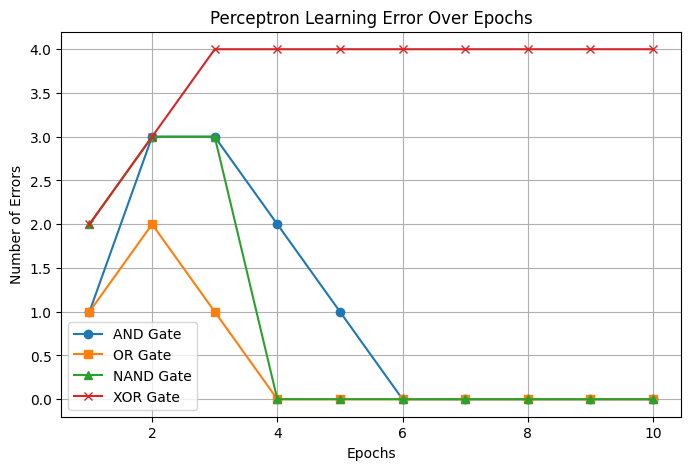
💬 Comment
- 퍼셉트론: 입력 벡터에 가중치를 곱한 합이 기준(0)을 넘는지 판단하고, 학습 과정에서는 틀린 만큼만 조정하며 선형 분리를 배우는 구조
- XOR은 선형 분리 불가능한 문제이기 때문에
단층 퍼셉트론으로는 해결할 수 없다. - 이를 해결하려면 다층 퍼셉트론(MLP)이나 비선형 변환이 필요하다.
💡 Code : MLP로 XOR 문제 해결
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
class MultiLayerPerceptron:
def __init__(self, input_size=2, hidden_size=4, output_size=1, lr=0.5, epochs=1000):
self.W1 = np.random.uniform(-1, 1, (input_size, hidden_size))
self.b1 = np.zeros((1, hidden_size))
self.W2 = np.random.uniform(-1, 1, (hidden_size, output_size))
self.b2 = np.zeros((1, output_size))
self.lr = lr
self.epochs = epochs
self.losses = []
def sigmoid(self, x):
return 1 / (1 + np.exp(-np.clip(x, -250, 250)))
def sigmoid_derivative(self, x):
return x * (1 - x)
def forward(self, X):
self.z1 = np.dot(X, self.W1) + self.b1
self.a1 = self.sigmoid(self.z1)
self.z2 = np.dot(self.a1, self.W2) + self.b2
self.a2 = self.sigmoid(self.z2)
return self.a2
def backward(self, X, y, output):
m = X.shape[0]
dZ2 = output - y
dW2 = (1 / m) * np.dot(self.a1.T, dZ2)
db2 = (1 / m) * np.sum(dZ2, axis=0, keepdims=True)
dZ1 = np.dot(dZ2, self.W2.T) * self.sigmoid_derivative(self.a1)
dW1 = (1 / m) * np.dot(X.T, dZ1)
db1 = (1 / m) * np.sum(dZ1, axis=0, keepdims=True)
self.W2 -= self.lr * dW2
self.b2 -= self.lr * db2
self.W1 -= self.lr * dW1
self.b1 -= self.lr * db1
def train(self, X, y):
for epoch in range(self.epochs):
output = self.forward(X)
loss = np.mean((output - y) ** 2)
self.losses.append(loss)
self.backward(X, y, output)
#if epoch % 200 == 0:
# print(f"Epoch {epoch}/{self.epochs}, Loss: {loss:.6f}")
def predict(self, X):
output = self.forward(X)
return (output > 0.5).astype(int)
def predict_prob(self, X):
return self.forward(X).ravel() # 결정 경계용
# === XOR 데이터 ===
X_xor = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y_xor = np.array([[0], [1], [1], [0]])
# === 학습 ===
print("\n=== XOR Gate Multi-Layer Perceptron Training ===")
mlp = MultiLayerPerceptron(input_size=2, hidden_size=2, lr=0.5, epochs=10000)
mlp.train(X_xor, y_xor)
# === 예측 결과 출력 ===
print("\nXOR GATE Test (Multi-Layer Perceptron):")
xor_predictions = mlp.predict(X_xor)
for i, x in enumerate(X_xor):
predicted = xor_predictions[i][0]
actual = y_xor[i][0]
result = "✓" if predicted == actual else "✗"
print(f"Input: {x}, Predicted: {predicted}, Actual: {actual}, {result}")
# === 결정 경계 시각화 함수 ===
def plot_decision_boundary(X, y, model, title="Decision Boundary"):
cmap_light = ListedColormap(['#FFDDDD', '#DDDDFF'])
cmap_bold = ListedColormap(['#FF0000', '#0000FF'])
h = .01
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
grid = np.c_[xx.ravel(), yy.ravel()]
Z = model.predict_prob(grid)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(6, 5))
plt.contourf(xx, yy, Z > 0.5, cmap=cmap_light)
plt.scatter(X[:, 0], X[:, 1], c=y.ravel(), cmap=cmap_bold,
edgecolor='k', s=120)
plt.title(title)
plt.xlabel("Input 1")
plt.ylabel("Input 2")
plt.grid(True)
plt.show()
# === 결정 경계 시각화 ===
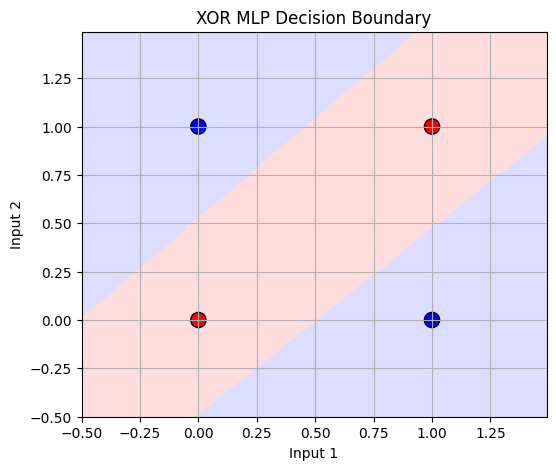
plot_decision_boundary(X_xor, y_xor, mlp, title="XOR MLP Decision Boundary")
# === 손실 곡선 시각화 ===
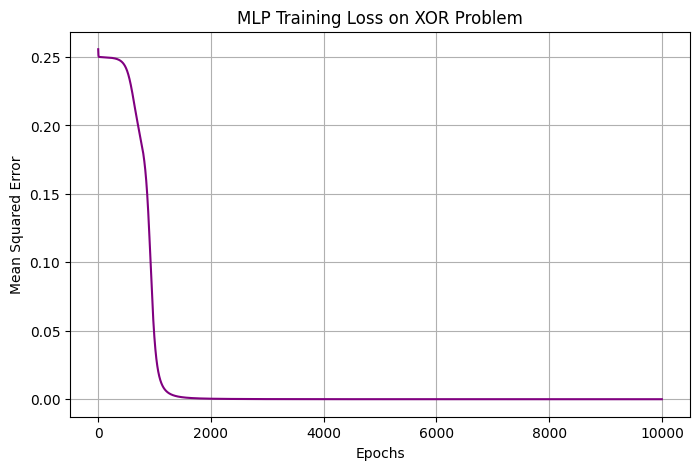
plt.figure(figsize=(8, 5))
plt.plot(range(mlp.epochs), mlp.losses, color='purple')
plt.title("MLP Training Loss on XOR Problem")
plt.xlabel("Epochs")
plt.ylabel("Mean Squared Error")
plt.grid(True)
plt.show()
✅ Result : MLP로 XOR 문제 해결
=== XOR Gate Multi-Layer Perceptron Training ===
XOR GATE Test (Multi-Layer Perceptron):
Input: [0 0], Predicted: 0, Actual: 0, ✓
Input: [0 1], Predicted: 1, Actual: 1, ✓
Input: [1 0], Predicted: 1, Actual: 1, ✓
Input: [1 1], Predicted: 0, Actual: 0, ✓